COVID-19 in der Schweiz Epidemiologische Analysen in Echtzeit powered by EpiGraphHub

Datenquellen

In dieser Arbeit haben wir Daten des Bundesamtes für Gesundheit (BAG) verwendet. opendata.swiss/en/dataset/covid-19-schweiz). Wir haben die gemeldeten Zahlen der täglichen Fälle (dargestellt in Abbildung 1), der Krankenhauseinweisungen, der Tests, der Testpositivität und der Todesfälle aus allen 26 Kantonen verwendet. Kantone sind Verwaltungsregionen in der Schweiz, ähnlich einem Land in den Vereinigten Staaten.

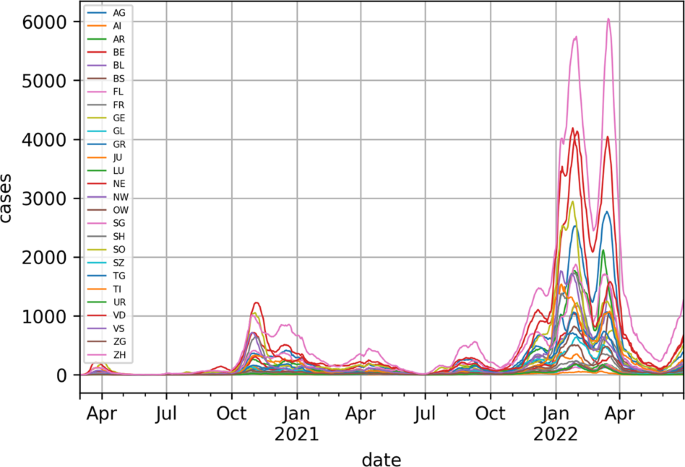
Alltagsthemen sind für alle Kantone wichtig. Wir können sehen, dass es Zeitverzögerungen zwischen den Inzidenzkurven gibt. Provinzen werden durch aus zwei Buchstaben bestehende offizielle Codes (de.wikipedia.org/wiki/ISO_3166-2:CH).

Die hier verwendeten Datensätze sind in Tabelle 1 aufgeführt, in der wir die Namen, Kurzbeschreibungen und Links beschreiben, auf die über die EpigraphHub-Plattform zugegriffen werden kann.⁴. Für jeden der Datensätze eine entsprechende Metadatentabelle (https://epigraphhub.org/tablemodelview/list/). Metadatentabellen haben denselben Namen wie die Tabellen, auf die sie sich beziehen, mit dem angefügten Suffix „_MetaAndere COVID-19-Datensätze, die vom Bundesamt für Gesundheit bezogen wurden, stehen ebenfalls zum Download und zur Visualisierung auf EpigraphHub zur Verfügung. Die Datensätze werden ohne Änderungen gespeichert und erneut geteilt.

Für eine kurze Visualisierung der hier verwendeten Datensätze siehe epigraphhub.org/superset/dashboard/p/yorXv7eBJAQ/.

Visualisierung der Hospitalisierungsraten

Angesichts der Abfolge von Virusvarianten und der Auswirkungen der Impfung seit Anfang 2021 besteht eine einfache und effektive Möglichkeit, die Entwicklung des Krankenhausrisikos im Laufe der Zeit visuell zu verfolgen, darin, die tägliche Beziehung zwischen der Anzahl neuer Krankenhauseinweisungen und der Anzahl neuer Krankenhauseinweisungen zu betrachten Pro Tag gemeldete Covid-19-Fälle. Diese Visualisierung kann mit einem einfachen Streudiagramm und der Anwendung einer temporären Farbzuordnung erreicht werden. Schließlich haben wir die Analyse in 3-Monats-Blöcke unterteilt, um die Entwicklung der durchschnittlichen Schwere der Fälle darzustellen (Abb. 2). Wir können diese Tarife nach Kantonen betrachten, um zu sehen, wie sie sich von den nationalen Tarifen unterscheiden (Abb. 3).

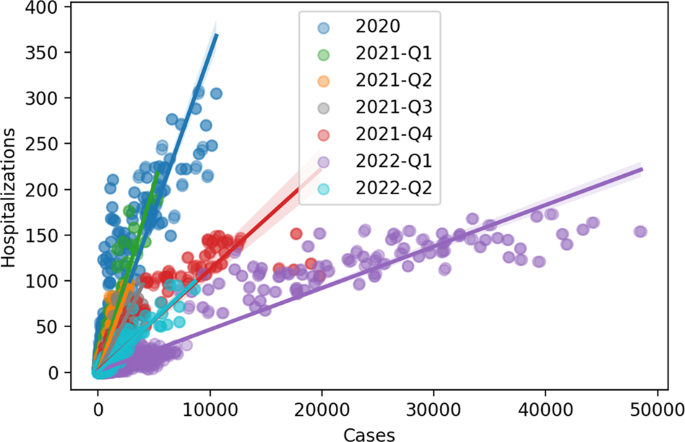
Tägliche Hospitalisierungen nach Fällen in der Schweiz, eingefärbt nach Quartilen (3-Monatsfenster). Q1: Januar-März, Q2: April-Juni, Q3: Juli-September und Q4: Okt-Dezember. Trendlinien stellen den mittleren Prozentsatz der Krankenhauseinweisungen für jeden Fall dar.

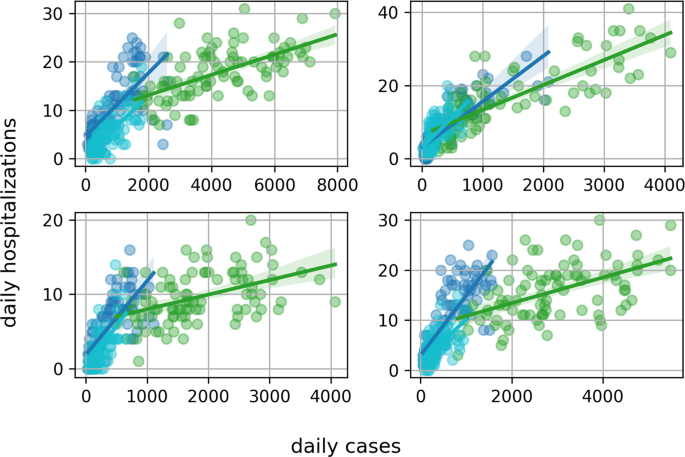
Fallweise täglicher Spitalaufenthalt in Zürich, Genf, Aargau und Bern. Die blauen Kreise stammen aus dem vierten Quartal 2021, die grünen Kreise aus dem ersten Quartal 2022 und Cyan aus dem zweiten Quartal 2022.

Räumliche und zeitliche Analyse

Aus täglichen Zeitreihen der gemeldeten Fälle für jeden Kanton haben wir eine paarweise Korrelationsanalyse angewendet, um die räumliche Dynamik des Virus aufzudecken.

Da sich das Virus über geografische Regionen (z. B. Kantone) ausbreitet, können Verzögerungen bei der Inzidenz von gemeldeten Fällen in verschiedenen Regionen abgeschätzt werden (Abb. 1). Wir haben die Kreuzkorrelation zwischen den täglich gemeldeten Serien neuer Fälle verwendet, um nicht nur diesen räumlichen Verlauf über die Zeit abzuschätzen, sondern auch um die Größenordnung der paarweisen Korrelationen zwischen allen Kantonen zu analysieren. zu spät kommen τ Zwischen zwei Reihen haben wir die Zeitverzögerung ausgewertet, die den Kreuzkorrelationskoeffizienten zwischen jedem Kantonspaar erhöht hat.

Die normalisierte Kreuzkorrelationsfunktion für zwei Zeitreihen, X_R Und die s_R gegeben von:

Zeichen τ was die Kreuzkorrelationsfunktion erhöht, ist ein Proxy für die Vorhersagbarkeitsrichtung, d.h. wenn ρ_{x y}(τ > 0) bedeutet Kanton X Erwarten von s in Inzidenztrends und kann daher ein guter Indikator für sein s ⁶. um einen Wert zu finden τdie die Korrelation für jedes Kantonspaar maximieren, haben wir berechnet ρ_{x y}(τ ) Werte τ Sie beträgt 30 bis 30 Tage. hier drüben, Mikrometer Und die σsind der Mittelwert und die Standardabweichung für jede Zeitreihe. Wir haben diese Informationen verwendet, um Vorhersagemodelle für jeden Kanton zu erstellen, wie unten beschrieben. Zu beachten ist, dass dieses Vorgehen keinen Beweis für einen kausalen Zusammenhang zwischen Paaren von geografischen Regionen darstellt⁷. Es ermöglicht jedoch die Identifizierung von Regionen, die zu kurzfristigen Vorhersagen von Trends in anderen Regionen beitragen können.

räumliche Montage

mit 1−obenstehendes (ρ_{x y}) als Distanz zwischen den Kantonen XUnd die s Wir können eine Agglomeration von Kantonen machen⁶, wobei die wie oben beschrieben erhaltene optimale Verzögerung berücksichtigt wird. Maximale Korrelationen und optimale Verzögerungen werden als Korrelations- bzw. Verzögerungsmatrizen gespeichert (Abb. 4, 5).

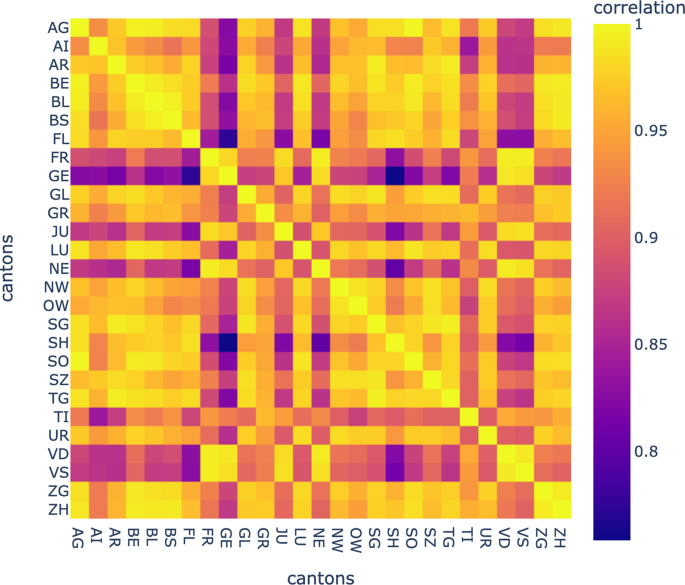
Kreuzkorrelationsmatrix kantonaler Vorkommenszeitreihen.

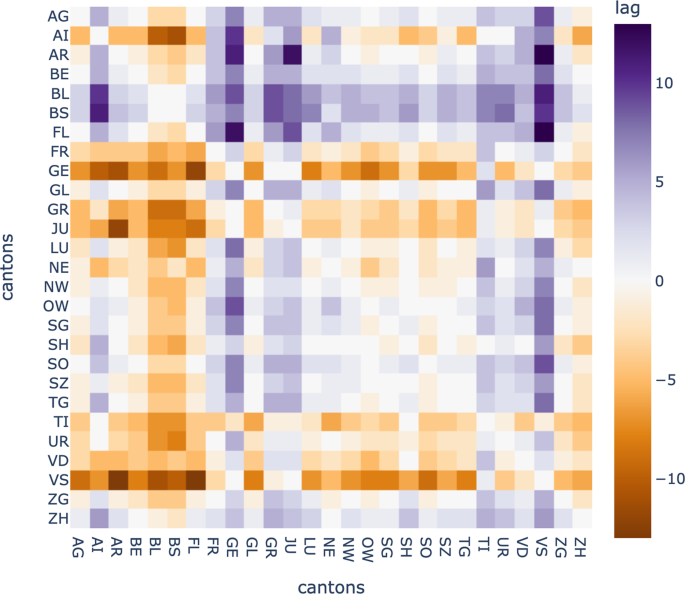
Diese Matrix zeigt die mit der Zeitverzögerung zunehmende Korrelation zwischen jedem Kantonspaar.

Schätzung der Prävalenz und Hospitalisierungsrate

Wenn wir uns Epidemien als zufällige Prozesse vorstellen, können wir die verfügbaren Daten verwenden, um Rückschlüsse auf ihre Häufigkeit zu ziehen. Hier haben wir Fälle, Tests und Krankenhausaufenthaltsreihen verwendet, um Prävalenz und Krankenhausaufenthaltsraten zu schätzen.

Die Schätzung der Prävalenz anhand der Anzahl der gemeldeten Fälle ist nicht trivial, da die Testhäufigkeit im Laufe der Zeit stark variiert, was sich auf die Anzahl der erkannten Fälle auswirkt. Daher haben wir ein einfaches hierarchisches Bayes’sches Modell konstruiert, um die Prävalenz von Infektionen abzuschätzen beste Freundin_R und Hospitalisierungsrate Ph.D_R der Anzahl der Tests t_R Die Anzahl positiver Tests (Fälle_R).

Wir beginnen mit der Modellierung der gemeldeten Fälle (Fälle_R) als Binomialoperation (Gl. 2) mit Parametern n Und die s Entspricht der Anzahl der täglichen Tests bzw. dem Anteil positiver Tests⁸.

Angenommen, wir gehen davon aus, dass die Anzahl der Tests und die Abdeckung des Tests groß genug sind, dass die getestete Population ungefähr einer repräsentativen Stichprobe der Allgemeinbevölkerung entspricht. In diesem Fall können wir anhand der Anzahl positiver Tests die Wahrscheinlichkeit abschätzen, dass der Test positiv ausfallen wird. Damit kann der Anteil der Infizierten an der Allgemeinbevölkerung angenähert werden, also die Prävalenzrate, beste Freundin_R. Um eine korrekte Darstellung des Spreads zu erhalten, können wir ihn mit Pre-Beta modellieren: \(P{v}_{t}\sim Beta \left({\alpha }_{p},{\beta }_{p} \right)\)technisch gesehen, als Zufallsvariable behandelt.

Auf ähnliche Weise können wir die Wahrscheinlichkeit eines Krankenhausaufenthalts wie folgt modellieren \(P{h}_{t}\sim Beta \left({\alpha }_{h},{\beta }_{h} \right)\) und Krankenhausaufenthalt als zweischneidiges,

Dann wird das vollständige Bayes’sche Modell zu:

Auswahl von nicht-informativer Beta-Software, \({\alpha}_{h}={\beta}_{h}={\alpha}_{p}={\beta}_{p}=0,5\)um die Schlussfolgerung von neutral zu beginnen a priori Eindruck.

Diese einfachen Wahrscheinlichkeitsmodelle enthalten einen Ausdruck in geschlossener Form für die A-posteriori-Verteilung binomialer Wahrscheinlichkeitsparameter, da sie auf konjugierten (beta-binomialen) Verteilungen basieren. Inferenz basierend auf den hier gezeigten Modellen wurde mit dem PyMC-Python-Paket (www.pymc.io) oder verwenden Sie geschlossene Formeln für nachfolgende Beta-Verteilungen.

Der Vorteil einer probabilistischen Darstellung der Inzidenz besteht darin, dass wir sie in das Binomialmodell der Krankenhauseinweisung einbinden können (Gleichung 3).

Vorhersagemodelle

Die Verwendung von Ensemble-Modellen zur Vorhersage von Epidemie-Zeitreihen wurde in den letzten Jahren mehrfach erfolgreich angewendet^6,9.

Um Krankenhausaufenthaltskurven in Kantonen vorherzusagen, haben wir ein probabilistisches Gradientenverbesserungsmaschinenmodell verwendet¹⁰da sie komplexe nichtlineare Beziehungen in Regressionsmodellen mit mehreren Zeitreihen erfassen können.

Das Modell ist definiert als

wo h_{k, t} Als gewöhnliche logarithmische Zufallsvariable modelliert, die Anzahl neuer Spitaleinweisungen im Kanton KIn einem Tag R Und die c es passiert, t ist die Anzahl der durchgeführten Tests, und Intensivstation ist die Zahl der Intensivpatienten. Jeder dieser Prädiktoren wird mit einer Verzögerung 14 Mal in das Modell aufgenommen τ= 1…14 (wir verwenden die letzten 14 Tage jeder Serie als Vorhersagen). In gleicher Weise können verschiedene Kantone derselben Gruppe wie z KSie werden auch mit den gleichen Verzögerungszeiten zum Modell hinzugefügt.

Gleichungsmodell. (4) kann trainiert werden, einen Krankenhausaufenthalt an jedem ≥ Tag vorherzusagenR. Wir haben es hier verwendet, um die Anzahl der Krankenhausaufenthalte bis zu 14 Tage früher vorherzusagen (Abb. 9).

Vorhersagemodelle werden täglich ausgeführt, unmittelbar nachdem die Daten in der EpiGraphHub-Datenbank aktualisiert wurden. Die Vorhersagen werden dann auch auf EpiGraphHub gespeichert. Die URLs der verwendeten aktualisierten Datensätze und die Ergebnistabellen sind in Tabelle 1 dargestellt.